
Similar to the logarithmic scale one can have a double logarithmic and super-logarithmic scale. 5, 3.162, 1453, 1e1453, 10^1e1453, notation of extremely large numbers.)įor extremely small numbers (in the sense of close to zero) neither method is suitable directly, but of course the generalized order of magnitude of the reciprocal can be considered. The "midpoints" which determine which round number is nearer are in the first case:ġ.076, 2.071, 1453, 4.20e31, 1.69e316.Īnd, depending on the interpolation method, in the second case (the first two mentioned, and the extension to the left, may not be very useful, the two just demonstrate how the sequence mathematically continues to the left). Rounding these downward to an integer gives categories between very "round numbers", rounding them to the nearest integer and applying the inverse function gives the "nearest" round number. SI units are used together with SI prefixes, which were devised with orders of magnitude in mind.įor extremely large numbers, a generalized order of magnitude can be based on their double logarithm or super-logarithm. This is useful for getting an intuitive sense of the comparative scale of familiar objects. The pages in the table at right contain lists of items that are of the same order of magnitude in various units of measurement. An order of magnitude estimate is sometimes also called a zeroth order approximation. For example, an order of magnitude estimate for a variable between about 3 billion and 30 billion (such as the human population of the Earth) is 10 billion. Thus, an order of magnitude is an approximate position on a logarithmic scale.Īn order of magnitude estimate of a variable whose precise value is unknown is an estimate rounded to the nearest power of ten. For example, 4,000,000 has a logarithm of 6.602 its order of magnitude is 6. More precisely, the order of magnitude of a number can be defined in terms of the decimal logarithm, usually as the integer part of the logarithm. Number of powers of 10 contained in the number. The order of magnitude of a number is, intuitively speaking, the Two numbers of the same order of magnitude have roughly the same scale: the larger value is less than ten times the smaller value. If they differ by two orders of magnitude, they differ by a factor of about 100. If two numbers differ by one order of magnitude, one is about ten times larger than the other. Orders of magnitude are generally used to make very approximate comparisons.
#Estimate the order of magnitude power of ten of series
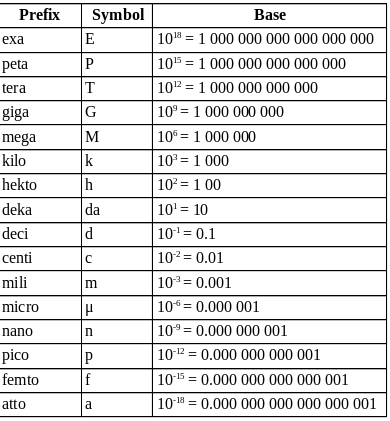
Usually, orders of magnitude refers to a series of powers of ten this article discusses the decimal scale. The ratios most commonly used are 1000, 10, 2, 1024 or e ( Euler's number, a transcendental number approximately equal to 2.71828182846 that is used as the base for natural logarithms). (Redirected from Order of magnitude) Orders of magnitudeĪn order of magnitude is the class of scale or magnitude of any amount, where each class contains values of a fixed ratio to the class preceding it.


 0 kommentar(er)
0 kommentar(er)
